Skip to main content

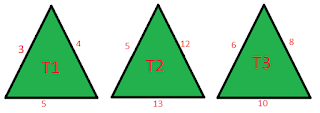
Show that the relation R defined in the set A of all triangles as R = {(T1 , T2 ) : T1 is similar to T2 }, is equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1 , T2 and T3 are related?



Class 12, NCERT Chapter 1,  Exercise 1.1, Q12


It is given that the relation R defined in the set A of all triangles as
R = {(T1, T2): T1 is similar to T2},
Now, R is reflexive as every triangle is similar to itself.

Now, if (T1, T2) ϵ R, then T1 is similar to T2.
⇒ T2 is similar to T1.
⇒ (T1, T2) ϵ R
Therefore, R is symmetric.

Now, if (T1, T2), (T2, T3) ϵ R,
⇒ T1 is similar to T2 and T2 is similar to T3.
⇒ T1 is similar to T3.
⇒ (T1, T3) ϵ R
Therefore, R is transitive.
Therefore, R is an equivalence relation.





Now, we can see that,


Therefore, the corresponding sides of triangles T1 and T3 are in the same ratio.

Thus, triangle T1 is similar to triangle T3.

Therefore, T1 is related to T3.
Labels:

Comments

Post a Comment

Popular posts from this blog

. Let f : R → R be defined as f(x) = 3x. Choose the correct answer. (A) f is one-one onto (B) f is many-one onto (C) f is one-one but not onto (D) f is neither one-one nor onto.

Class 12, NCERT Chapter 1,  Exercise 1.2, Q12 f : R → R defined as  f ( x ) = 3 x . Let  x ,  y  ∈  R  such that  f ( x ) =  f ( y ). ⇒ 3 x  = 3 y ⇒  x  =  y ∴ f  is one-one. Also, for any real number ( y)  in co-domain  R , there exists  in  R  such that . ∴ f  is onto. Hence, function  f  is one-one and onto. The correct answer is A.
1 comment
Read more

Let f : N → N be defined by f (n) ={ (n+1)/2, if n is odd and (n-1)/2, if n is even, for all n ∈ N.State whether the function f is bijective. Justify your answer

Class 12, NCERT Chapter 1,  Exercise 1.2, Q9 Thus it is bijective.
Post a Comment
Read more